BitcoinのUTXOセットを管理するにあたって、そのストレージ要件を大幅に削減すると期待されているアキュムレータ。昨年のScaling Bitcoinでは、スタンフォード大学のBenedikt BünzがRSAを利用したアキュムレータを紹介した↓
techmedia-think.hatenablog.com
↑はその性質上Trusted Setupを必要とするという課題があり、Trusted Setupを回避するためにClass Groupを使用するという提案もあるがまだ新しい暗号プリミティブであるという課題はある。
そんな中、今回Lightning Networkのホワイトペーパーの共著者でもあるThaddeus Dryjaがマークルツリーを利用したハッシュベースのアキュムレータ「Utreexo」を発表した↓
https://eprint.iacr.org/2019/611.pdf
アキュムレータの構造
Utreexoは、要素のセットを完全二分木のフォレスト(森=複数の完全二分木が存在する)で管理する。
例えば要素の数が3つある場合、以下の2つのツリーが構成される。
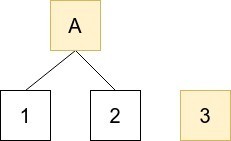
Aは1,2の要素から生成された親ノードのハッシュ値。この場合、アキュムレータは各ツリーのルートであるAと3の値を管理できれば良い。
要素の追加
さらに要素4を追加すると、フォレストは以下のような1つのツリーになる。
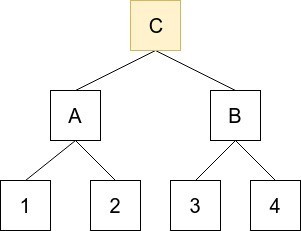
この場合、アキュムレータはルートCの値だけ管理すれば良い。
さらに要素5を追加すると、2つのツリーになり、アキュムレータはCと5を管理する。
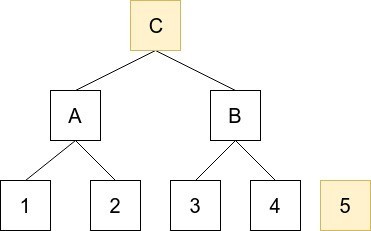
このような形で、アキュムレータは要素を完全二分木になるよう追加していく。新しく要素を追加する際も、各ツリーのルートハッシュだけ知っていれば新しいフォレストを構成できる。
この完全2分木の構造には効率的な特性がある。要素の数=リーフの数さえ分かれば、どのようなフォレストが構成されるかはリーフの数をバイナリ表現にすると明白になる例えば上記の要素の数5を例にすると、そのバイナリ表現は101となる。フォレースと内のツリーの数はこのバイナリ表現の1が立っているビットの数と等しく、それらの木の高さはbit 1が立っている位置から分かる。例えば、101であれば、そこから高さ1と高さ3のツリーが2つあることが分かる。
要素の包含証明
要素の追加については↑のようにフォレストの各ツリーのルートハッシュを管理すればいいことが分かったので、続いて要素の証明について。
要素がアキュムレータ内に存在するかどうかは包含証明(inclusion proof)を提供することで証明する。
この包含証明は
- リーフの位置
- ハッシュのリスト
で構成される。ハッシュのリストには、その要素が存在するツリーにおいて、その要素の兄弟のハッシュと、さらにそこからルートのハッシュを計算するのに必要な中間ノードのハッシュが含まれる。
アキュムレータと包含証明が与えられると、アキュムレータは要素の総数からフォレストの構成を知っているので、包含証明内のリーフの位置から、対象の要素がフォレスト内のどのツリーに属するものか判断する。ツリーが特定できると後は、包含証明のハッシュのリストと、アキュムレータが管理しているそのツリーのルートハッシュを使って、要素がアキュムレータ内に存在するか検証する。
例えば↑の5の要素があるツリーにおいて、要素3の包含証明は、
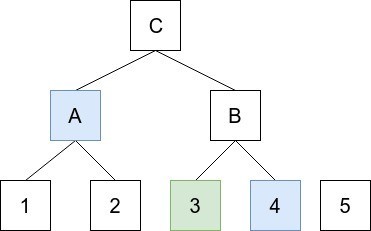
3の位置と、要素3と、その兄弟である4のハッシュと、さらにルートを計算するのに必要なAのハッシュとなる。これらの包含証明からルートハッシュを計算し、それがアキュムレータの管理するハッシュと等しければ要素がアキュムレータ内に存在することが分かるという仕組みだ。この辺のマークルツリーの復元とルートハッシュの計算は、現在のBloom Filterを利用したSPVクライアントがブロック内のトランザクションの有無を検証する手法と基本的に同じだ。
要素の削除
削除する際は、アキュムレータにその要素の包含証明(inclusion proof)が与えられ、該当する要素がアキュムレータ内に存在するか検証し、存在する場合要素を削除する。Bitcoinでは、あるトランザクションでUTXOが消費された場合にそのUTXOの包含証明が添付され、アキュムレータに対して要素の存在検証が終わったのち、アキュムレータから要素を削除する。このようなケースは基本的に新しいブロックを受信した際に行われ、その際には大量の新規UTXOの追加と大量の既存UTXOの削除が行われる。このため1つ1つの要素をアキュムレータから削除し都度アキュムレータを更新するよりも、削除対象の要素のセットを一括で処理してしまう方が必要なハッシュ計算の回数が少なくて済む。
削除では以下のTwin、Swap、Root、Climbという4つのステップ順番に繰り返す。
Twin
まず最初に処理されるのがTwinで、左右の兄弟両方が削除される場合の削除を指す。
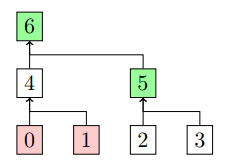
例えば↑の場合、0と1が削除対象のリストに入っている要素。Twinで削除されると更にその親の要素4が削除リストに加えられる。
Swap
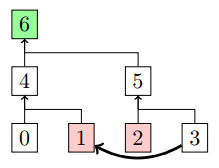
↑のように要素1, 2が削除対象な場合、要素3の要素1があった場所に移動する。そして親の5は次の行を処理する際の削除リストに追加される。
この時ノードは要素3のハッシュ値について知っている必要があるが、ツリーのルート値しか知らないアキュムレータにはそれが分かるのか?と疑問に思うかもしれないが、要素3のハッシュ値は要素2を削除する際の包含証明で与えられているのでそれを利用する。
Root
TwinやSwapが起きるのはその行に対して偶数数の削除が発生する場合だ。削除の要素数が偶数の場合Rootステップはスキップされる。逆に要素の削除数が奇数の場合、Twin、Swapフェーズ終了後1つの削除要素が残った状態になり、この削除要素はRootステップで処理される。
Rootステップでは、処理する行にルートが存在する場合、ルートを削除の位置に移動する。
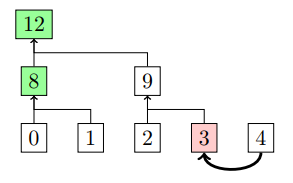
↑の場合、要素3が削除されているが同じ行にルート要素4があるので要素4を3の位置に移動して終了。
その行にルートが存在しない場合は、削除対象の兄弟をその高さのルート位置に移動し、フォレスト内に新しいツリーを作成する。
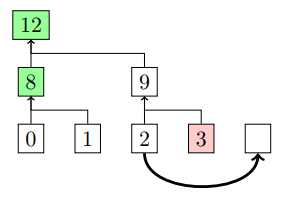
↑の場合、要素2は高さ1のツリーのルートに昇格する。2があった位置は削除対象になる。そのため2,3の削除がTwinに該当するので、その親の9も次の行での削除対象としてマークされる。
Climb
Rootステップが終了すると、Climbステップではフォレストのレベル間を移行する。各ステップを適用し移動後の親の再計算や削除が終了すると、ツリーの1つ上のレベルに上がってまたTwinから始める。これをフォレストの頂点に達するまで続ける。
Bitcoinへの適用
UTXOモデルを採用しているBitcoinでは、トランザクションには、インプットとアウトプットがあり、インプットは以前に作られたアウトプットを参照し使用する。この設計では、データ・セットに対する唯一の操作は作成、読み取り、削除で、記録後の要素のセットには削除以外に変更を加えることはできない。新しいトランザクションによって既存のUTXOが消費され新しいUTXOが誕生する。Bitcoinのフルノードはこの状態変化をすべて検証している。IBDと呼ばれる初期同期プロセスでは、ユーザーは200GBを超える履歴をダウンロードし、何億ものデジタル署名を検証する必要がある。そして最終状態においてそのUTXOセットは4GB近くになる。
現在のBitcoinのフルノードはUTXOセットをディスク上のデータベースに保存している(levelDB)。このUTXOは作成されてから使用される直前までの期間、システムに影響を与えずデータベースエントリーにアクセスされることもなく、それが使用される場合のみディスクから読み取られる。
そのため、消費されるまでアクセスされないUTXOを保存しなくて済む設計でにできると、フルノードを運用するハードウェア要件が緩くなる。現在でもRaspberry Piなんかの小型デバイスでフルノードを動かすことはできるが、基本的にUTXOセットにはサイズ制限が無いので、将来的に利用者の増加に伴いUTXOセットの膨張が進むかもしれない。このためUTXOの管理をアキュムレータ化すると、長期的なスケーラビリティに貢献することになり、またディスクの読み書きが最小限に抑えられることでIBDの同期時間の向上にもなる。
ブリッジノード
ただ、Bitcoinはもともとアキュムレータネイティブな設計ではなく、既に稼働中のBitcoinノードが多数ある状況で、当然そのノードもこのアキュムレータを実装している訳ではない。アキュムレータに対応したノードは、トランザクションを検証する際に別途UTXOの包含証明を添付する必要がある。アキュムレータに対象したノードであれば自身が所有するUTXOの包含証明を提供することができるが、他のノードはそれを要求しないだろうし、他のノードが伝播したトランザクションには包含証明が含まれていないのでアキュムレータ対応ノードはそれを検証できないといったことになる。
このため、現在稼働中のフルノードとアキュムレータに対応したノードが同時に稼働するためにはネットワークにブリッジノードが必要になる。ブリッジノードというのはアキュムレータ内の全てのUTXOに対するプルーフを持っているノードだ(Utreexoの場合マークルフォレスト全体を常に持っているノード)。
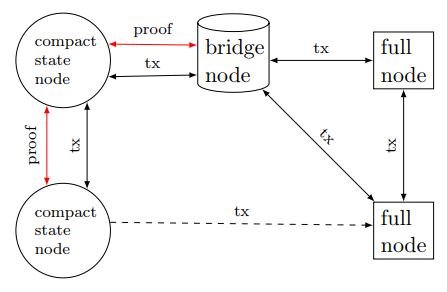
ブリッジノードは上記のように現状のフルノードとアキュムレータに対応したCompact State Nodeとのブリッジとして機能する。フルノードは以前と同様に動作し、トランザクションとブロックをお互いに伝播する。ブリッジノードはフルノードで、マークルフォレスト全体も格納し、Compact State Nodeに包含証明を提供する。Compact State Nodeは包含証明を省略することでトランザクションメッセージをフルノードに送信できるが、証明を提供できないフルノードから直接トランザクションを受け取ることはできない。
RSAアキュムレータと違ってTrusted Setupは必要ない。ただ、アキュムレータがフォレストのツリーのルートハッシュで構成されるので、ツリーの数の増減に伴いアキュムレーターのサイズも増減するので固定サイズにはならない。